Indikatoren wie gleitende Durchschnitte und Stochastik versuchen gewöhnlich, sich einem Markt anzupassen. Sie funktionieren möglicherweise nicht in allen Marktbedingungen und besitzen keine wesentlichen Eigenschaften, die der Markt befolgen muss.
Das entspricht allerdings nicht der Tatsache bei Fibonacci. Das Außergewöhnliche an Fibonacci meiner Meinung nach ist, dass die Fib Relationen ein grundsätzlicher Teil von natürlichen Systemen, einschließlich den Märkten, sind. Fibonacci Verhältnisse haben keine Vorlieben für bestimmte Markbedingungen oder Konjunkturzyklen. Fib Relationen versuchen auch nicht, sich einem bestimmten Stil oder Markt anzupassen; sie sind vielmehr ein natürlicher Teil der Marktbewegungen.
Das macht Fibonacci robust, beweglich und zeitlos.
Eines meiner Lieblingsszenarien von Fibonacci ist eine Kursumkehr auf die 88.6% Ebene. Diese Stufe wird erreicht, indem man den 61.8 Fib Goldenen Schnitt nimmt, die Quadratwurzel davon berechnet und von dem Ergebnis nochmals die Quadratwurzel nimmt.
Ein Retracement (Korrektur - Welle) besteht aus einer Anfangsbewegung, einer Umkehr von dieser ersten Bewegung und einer anschließenden Fortsetzung der ersten Trendrichtung, wie es in dem folgenden Beispiel gezeigt wird:
Fibonacci - Der Führende Marker
Wenn Ich also sage, "Das ist ein 88.6% Fibonacci Retracement", bedeutet das nichts anderes, als dass die Umkehr 88.6% von der Größe der Anfangsbewegung ausmacht. Falls die Anfangsbewegung 100 Pips aufwärts ergibt, würde das Retracement 88.6 Pips nach unten betragen. Es spielt keine Rolle, ob die Anfangsbewegung nach oben oder nach unten zeigt.
Hier sind einige Beispiele von dem 88.6 Fibonacci Retracement.
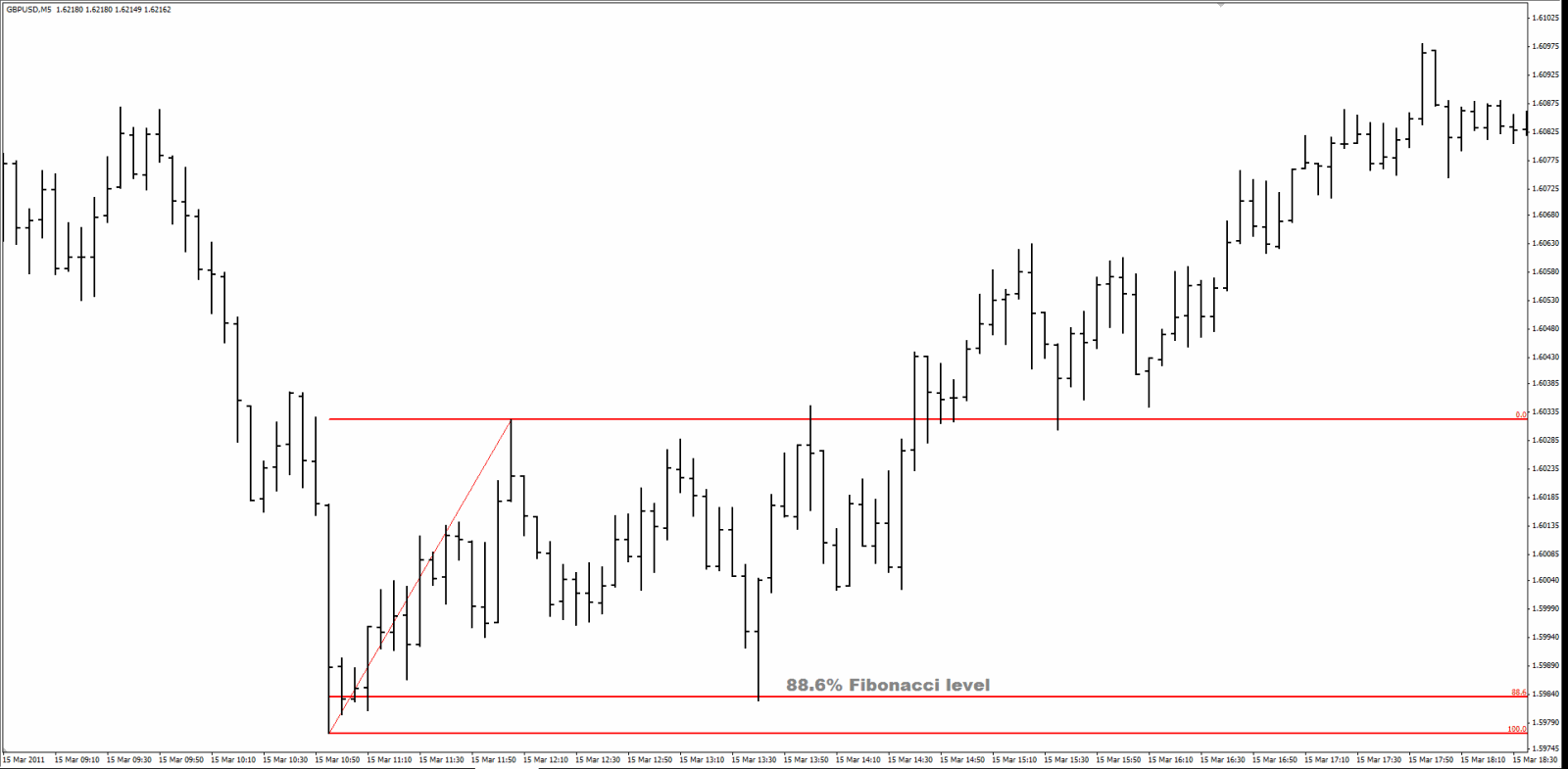
Zunächst ein 5 Minuten GBP - USD Diagramm, bei dem die Anfangsbewegung nach oben zeigt, gefolgt von einem nach unten zeigenden Korrektur - Welle.
Fibonacci - Der Führende Marker
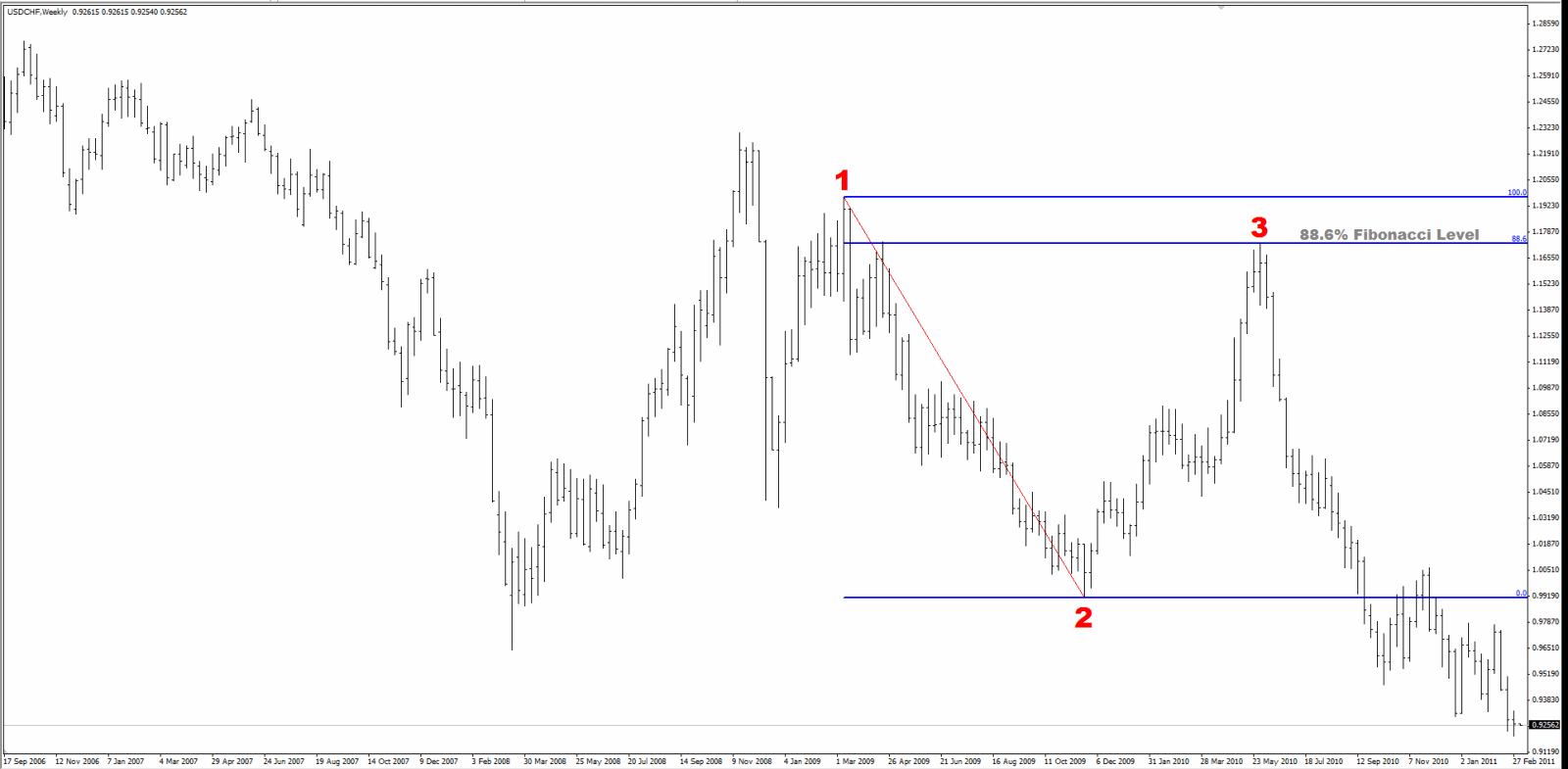
Dies ist ein Wochen USD-CHF Chart, wo die Anfangsbewegung nach unten zeigt, gefolgt von einem ansteigenden Retracement.
Fibonacci - Der Führende Marker
Das ist ein ausgezeichnetes Beispiel von der Genauigkeit der Fibonacci Ebenen. Nach der abwärtszeigenden Anfangsbewegung steigt der Kurs in einem Zeitraum von 27 Wochen 1.821% Pips an und trifft die Fibonacci Ebene innerhalb von 2 Pips! Diese Konfigurationen ermöglichen es den Händlern, über Trades zu verfügen, die über 1,000 Pips einbringen, während sie ihr Risiko weiterhin unter Kontrolle haben.
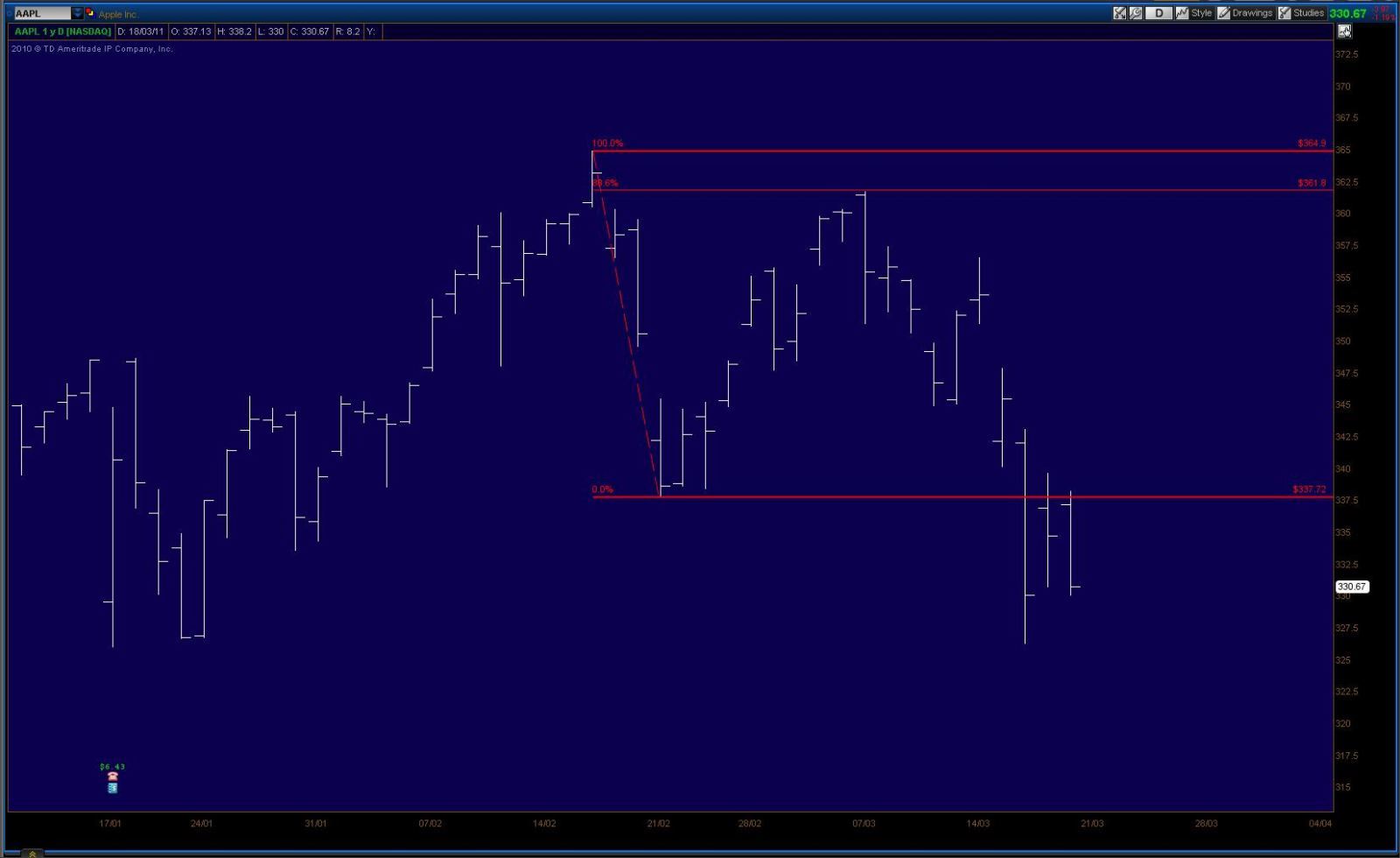
Und nur um die Vielseitigkeit quer durch die Märkte zu zeigen, dies ist das Tagesdiagramm von der NASDAQ Aktie, Apple (Symbol: AAPL):
Fibonacci - Der Führende Marker
Hier fällt der Aktienkurs in vier Tagen über $27, dann steigt er innerhalb einiger weniger Cents auf die 88.6 Ebene an, bevor er wieder fällt.
Wenn Ich ein Fibonacci Retracement handle, lasse Ich den Kurs die Ebene erreichen und bewege mich innerhalb einer oder zwei Balken von dem Zeitrahmen, den Ich benütze, weg; i.e. Ich hänge nicht bei dieser Ebene mehrere Balken lang herum. In den drei oben gezeigten Beispielen erreicht der Kursbalken die 88.6 Ebene einmal, und nur einmal. Zweitens bin Ich der Meinung, man sollte man die Ebene bedingungslos respektieren: der Kurs sollte nicht erheblich in die Ebene eindringen; er sollte stattdessen die Ebene genau treffen.
Ich handle immer mit einem Stop und mein Erfolgsziel ist dort, wo die Umkehr beginnt, i.e. am Ende der Anfangsbewegung rauf oder runter. Häufig übertrifft der Kurs dieses Ziel, aber Ich bin glücklich, meinen Profit an dieser Stelle einzunehmen. Ich handle diese Konfiguration nur mit einem guten Risiko/Belohnung Verhältnis, normalerweise 1:2 oder größer. Wenn Ich keine Stelle finde, wo ich meinen Stop in einer vernünftigen Entfernung im Vergleich zu meinem Ziel platzieren kann, verzichte Ich auf den Trade.
Was können wir also über Fibonacci lernen?
1. Fibonaccis Grundlagen sind zeitlos. Sie werden Fibonaccis Ideen weder optimieren noch aufgeben müssen, wenn die Märkte sich ändern.
2. Fibonaccis Grundlagen können von dem kleinsten bis zu dem größten Zeitrahmen verwendet werden.
3. Fibonacci hat keine Neigung für bestimmte Märkte; Sie können sie auf alles, was ein Diagramm besitzt, eine Aktie, ein Währungspaar, ein Metall und sogar ein komplexes Derivat, anwenden.